おみやげ算の計算については、機械的に暗記して使っている方がほとんどだと思います。
「なぜそのような計算方法になるのか?」を知りたい方向けに、おみやげ算をわかりやすく図で証明したいと思います。
おみやげ算は証明できるのか?
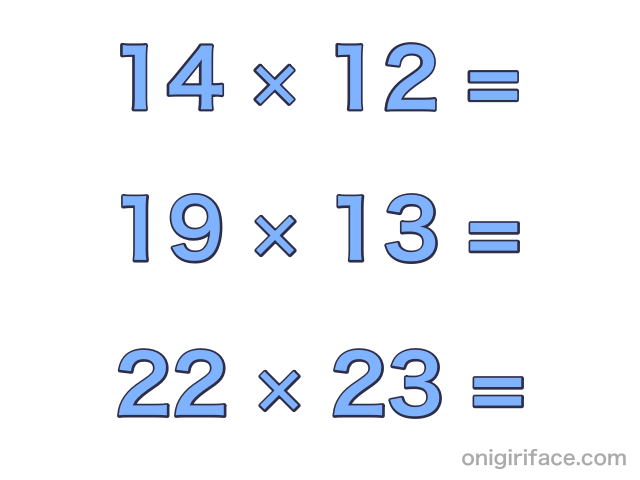
「おみやげ算は証明できるのか?」についてですが、中学3年生で学習する乗法公式(式を展開する公式)を使うと証明できます。
※乗法公式とは(X+a)(X+b)のような公式。
例えば14×12の場合、前半の式は「16×10」になりますが、これは乗法公式だと(14+2)(12-2)となります。
しかしおみやげ算を使うのは主に小学生。まだ習っておらず理解できないと思うのでこれ以上は割愛します。
小学生にもわかりやすく図を使って証明します。
おみやげ算をわかりやすく図で証明
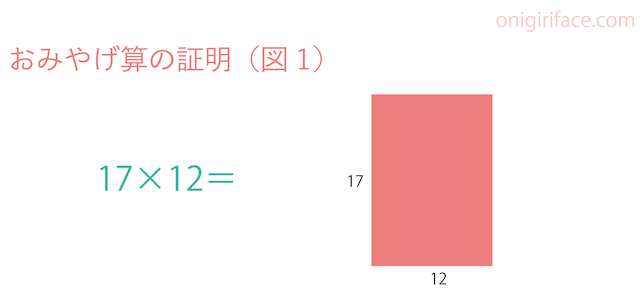
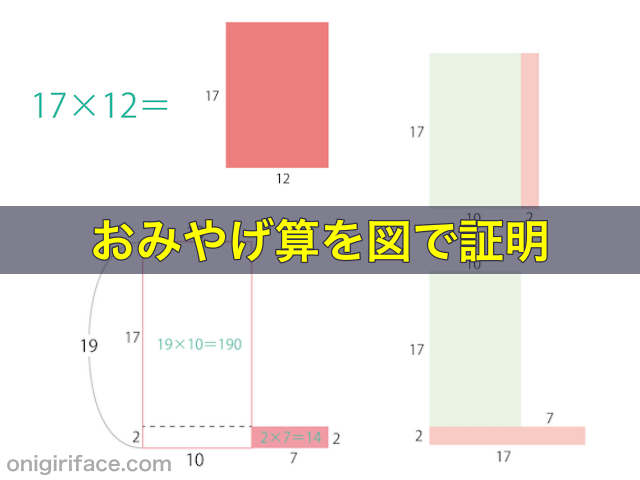
17×12=を例におみやげ算を証明していきます。
17×12=は縦×横の掛け算です。図で表すと「図1」の四角形になります。
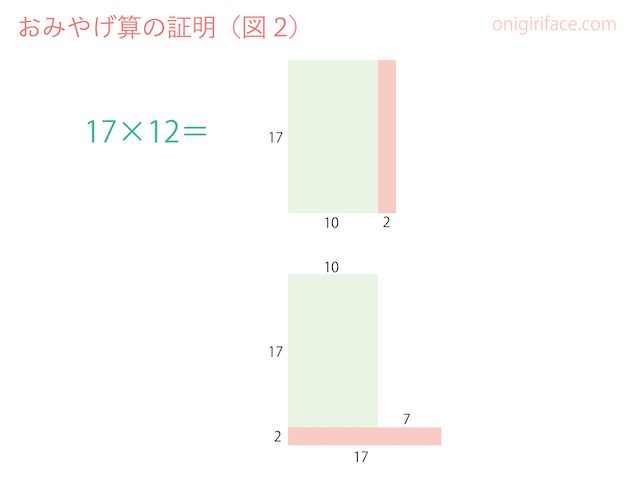
図1の四角形の横の数字(掛ける数)「12」を「10×○」に分割すると、図2の上の絵のように「10と2」に分けられます。
この数字の2の方の数(1桁の数)を横に倒したのが、図2の下の絵になります。
少しだけ右側が飛び出していることから、四角形が2つあることがわかります。
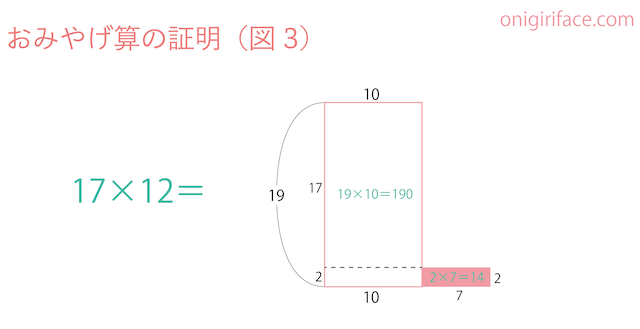
図2を左側の四角形と右側の(飛び出した)四角形に分けたのが「図3」の絵です。
左の四角形は19×10=190と暗算で解けますね。これがおみやげ算の最初の計算の部分です。
そして右側の(飛び出した)四角形はおみやげ算の次にする計算です。ここでは2×7=14になりました。
この2つ目の計算「2×7=14」は、17×12の1桁同士の掛け算であることがわかります(※)
※縦×横は先程倒したので逆になっていますが、答えは同じになります
「最初の計算(掛け算)」と「次の1桁同士の掛け算」の後に足し算をするというのがおみやげ算でしたね。
それが上の図で証明されました。
最後に
おみやげ算はそれぞれを計算(掛け算)をした後に、最後に両方の数を足すのはなぜなのか?というのが図で理解できたかと思います。
機械的に暗記して計算していますが、以上ような理由から成り立っています。
最後の足し算をするのを忘れがちですが、上の図を思い出すとこれからは忘れずに計算できると思います。
関連:おみやげ算をわかりやすく図解!14×13を簡単に暗算する方法
学習に興味がある方は下の記事も続けて読んでみて下さい▼
