消去算のやり方｜練習問題をわかりやすく図説｜中学受験対策

算数の中学受験で出題される文章題をできるだけわかりやすく早くに解く方法をブログにまとめています。

今回は消去算についてです。

消去算のわかりやすい解き方、練習問題（2問）を使って図説しています。

 

消去算とは？

消去算とは（リンゴとミカンなど）2つの物の合計金額がわかっていて、それが2パターンあり、複数の式をもとに1個あたりの値段を求める問題です。

最小公倍数で同じ数にすることで、片方を消去し置き換えられるという意味から来ています。

前回解説した「つるかめ算」と文章題は似ていますが、消去算の場合は複数の式があり、最小公倍数を求め、代入し（置き換え）、式を移動させることによって求めるところが異なります。

本当は中学校の連立一次方程式で習いますが、最小公倍数を習う小学5年生の教科書にも考え方が載っていることから、中学受験で多く出題されています。

関連：消去算は小学何年生で習うの？時間をかけて習わないのはなぜ？

中学受験対策としての具体的な解き方を2つの練習問題を使って解説していきます。

 

消去算のわかりやすい解き方｜練習問題で解説

ここからは消去算のわかりやすい解き方を、練習問題（2問）で解説します。

消去算の練習問題1と解説

練習問題1を図を使って解説します。文章題を式にすると以下のようになります。

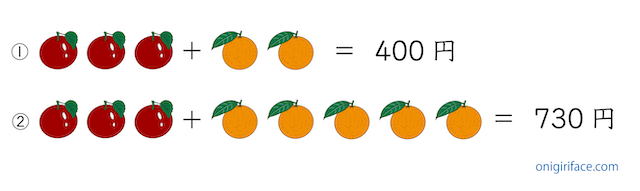
• リンゴ3個＋ミカン2個＝400円
• リンゴ3個＋ミカン5個＝730円

この問題は、2つの式どちらにも「リンゴが3個」なので、この場合の解き方が簡単。消去算の基礎問題になります。

 

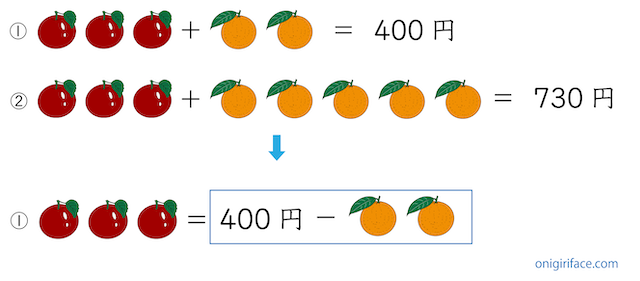
どちらも「リンゴが3個」。①のミカン2個を移動させると「リンゴ3個＝400円−ミカン2個」となります。

 

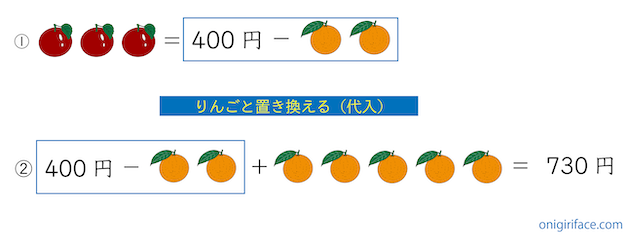
「リンゴ3個＝400円−ミカン2個」なので、②の式にある「リンゴ3個」のところに、「400円ーミカン2個」を代入します（置き換える）。

これにより「400円−ミカン2個＋ミカン5個＝730円」となりました。

 

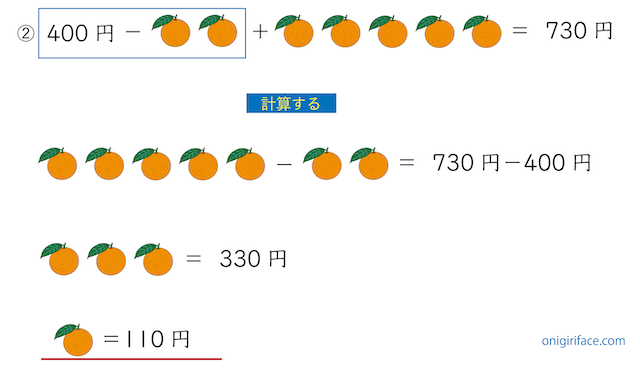
「400円−ミカン2個＋ミカン5個＝730円」と、式がミカンだけになったので、移動させてミカン1個あたりの値段を計算します。

1. ミカン5個−ミカン2個＝730円−400円［引き算する］
2. ミカン3個＝330円［割り算し1個あたりを求める］
3. ミカン1個＝110円

ミカン1個は110円になりました。

 

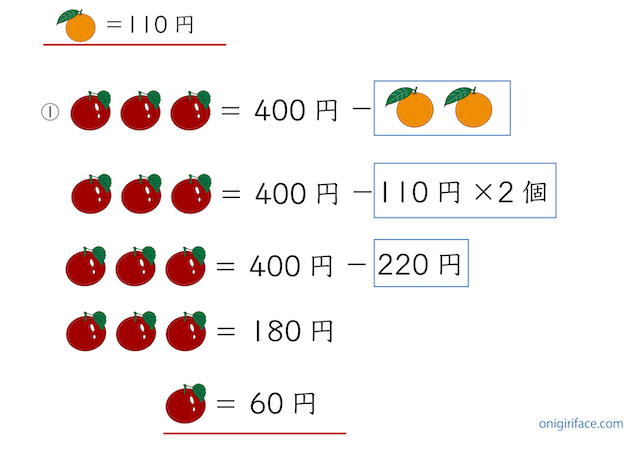
ミカン1個が110円であることがわかったので、最初の①の式に代入します。

1. リンゴ3個＝400円−ミカン2個
2. リンゴ3個＝400円−110円×2個［ミカン1個の値段に置き換える（代入）し、掛け算する］
3. リンゴ3個＝400円−220円［引き算する］
4. リンゴ3個＝180円［割り算し1個あたりを求める］
5. リンゴ1個＝60円

リンゴ1個は60円であることがわかりました。

以上の解き方から「リンゴ1個は60円、ミカン1個は110円」という答えになります。

この文章題は最初からリンゴの数が同じだったので、解くのは簡単でした。（教科書に載っている、考え方を学ぶ基礎問題）

実際に中学受験として出題されるのは次の練習問題2のような問題になります。

 

消去算の練習問題2と解説

練習問題2を図を使って解説します。文章題を式にすると以下のようになります。

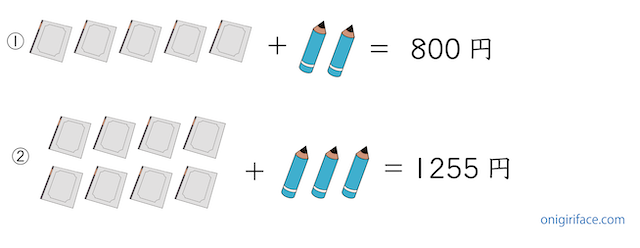
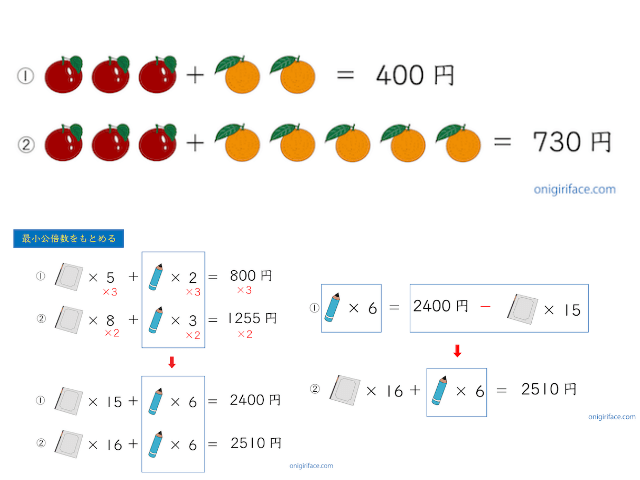
• ノート×5冊＋鉛筆×2本＝800円
• ノート×8冊＋鉛筆×3本＝1255円

まず最初に文章題を式にします。上の図を数字に変更してみたのが下の図です▼

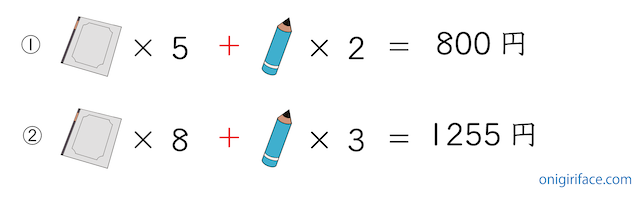
テスト問題を解く時は、ノートを「ノに◯をつける」、鉛筆を「えに◯をつける」などして工夫して下さい。

 

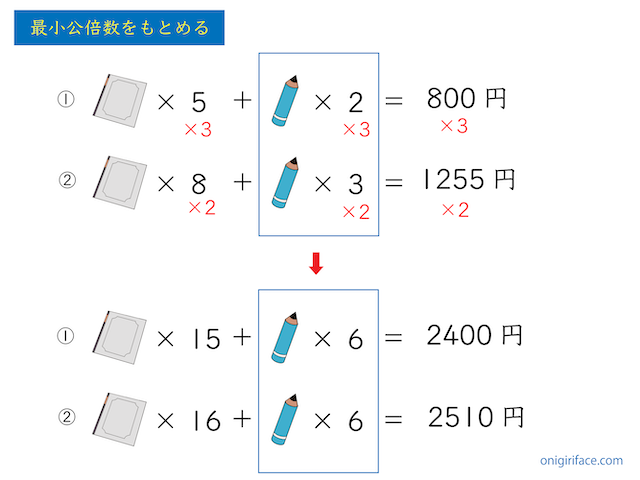
「練習問題2」は「練習問題1」とは違い、同じ数のものがないため、最小公倍数を使う必要があります。

ノート1冊は何円か求める問題なので、ノートの最小公倍数をもとめます。

①の鉛筆2本を「×3」に、②の鉛筆3本を「×2」し、鉛筆を6本に統一します。

• ノート×15冊＋鉛筆×6本＝2400円（それぞれ×3）
• ノート×16冊＋鉛筆×6本＝2510円（それぞれ×2）

 

①ノート×15冊＋鉛筆×6本＝2400円の「ノート×15冊」を右に移動させます。

• 鉛筆×6本＝2400円−ノート×15冊

鉛筆6本は「2400円−ノート×15冊」と同じなので、②の式に代入します（置き換える）。

• ノート×16冊＋鉛筆×6本＝2510円
  →ノート×16冊＋2400円−ノート×15冊＝2510円

 

最後に計算し、ノート1冊あたりの値段を求めます。

• ノート×16冊＋2400円−ノート×15冊＝2510円
• ノート×16冊−ノート×15冊＝2510円−2400円（2400円を右に移動）
• ノート×1冊＝110円（引き算する）

引き算するとノート1冊は110円であることがわかりました。

以上の解き方が、消去算になります。

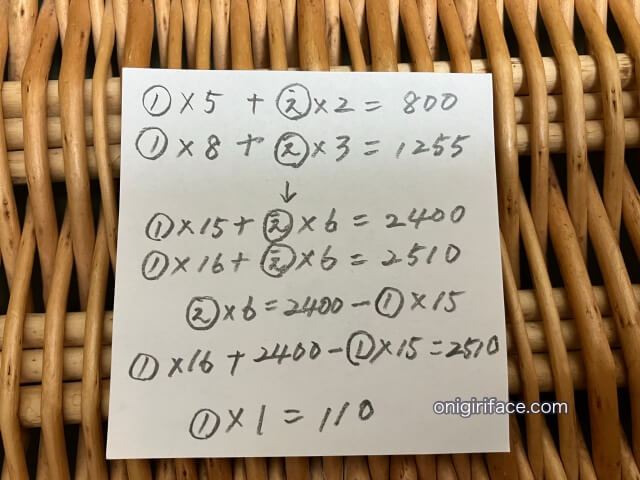
▲実際に練習問題2を解いてみました。中学受験対策として、実際に鉛筆を使って解く練習をして下さい。

 

最後に

消去算の解き方をわかりやすく図解しました。

練習問題1は同じ本数だったのでわかりやすかったと思いますが、練習問題2になると最小公倍数で同じ数にしてあげる必要があります。

中学受験ではこの練習問題2のような問題が多いので、練習問題2と似た問題を複数解いて慣れていくようにしましょう。

 

学習に興味がある方は下の記事も続けて読んでみて下さい▼

関連：小学生通信教育教材8社を比較！2024年おすすめランキング

 

インド式計算という暗算で解く方法をまとめています▼

関連：インド式計算 一覧まとめ